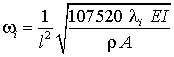|
Demonstrationsbeispiel zum
Wie das Matrizeneigenwertproblem für diese Aufgabe erzeugt wird, wird ausführlich auf der Seite "Eigenschwingungen mit der Finite-Elemente-Methode" beschrieben. Für den skizzierten Biegeschwinger gilt: Nach der Lösung des Allgemeinen Matrizeneigenwertproblems
können die Eigenkreisfrequenzen des Biegeschwingers aus den Eigenwerten λi nach der Formel
berechnet werden. Die Eigenvektoren, die die Lösung des Matrizeneigenwertproblems liefert, beschreiben die zugehörigen Schwingungsformen. Das aber ist für die hier zu demonstierenden Aussagen zu den Matrizeneigenwertproblemen uninteressant, trotzdem noch eine Bemerkung zum Berechnungsmodell: Ein kontinuierlich mit Masse belegter Biegeträger hat unendlich viele Eigenfrequenzen. Die analytische Lösung, die für dieses einfache Problem noch möglich ist, liefert sie alle (wird ausführlich behandelt im Skript "Biegeschwingungen gerader Träger"). Dass das Matrizeneigenwertproblem nur 7 Eigenwerte (und damit 7 Eigenkreisfrequenzen) liefert, liegt an dem recht groben Finite-Elemente-Modell, das allerdings für die Berechnung der kleinsten Frequenzen völlig ausreichend ist. |
Interaktive Lösung des Problems
Die bequemste Art, das oben formulierte allgemeine Matrizeneigenwertproblem zu lösen, ist die Nutzung des unter "Technische Mechanik - interaktiv" angebotenen Programms "Symmetrisches Matrizeneigenwertproblem". Nach Start des Programms wird zunächst auf das Eingabeschema "... allgemeines Matrizeneigenwertproblem" umgestellt, für die "Zeilen-/Spalten-Anzahl der Matrizen" wird der Wert 7 eingegeben:

Nach Anklicken von "OK" erweitert sich das Eingabeschema entsprechend, und die beiden Matrizen können eingegeben werden. Dabei müssen jeweils nur die Elemente für das rechte obere Dreieck der symmetrischen Matrizen eingegeben werden, die Elemente im linken unteren Dreieck werden automatisch ergänzt. Nach kompletter Eingabe wird "Rechnung starten" angeklickt, und der Bildschirm sollte so aussehen:

Die Eigenwerte sind der Größe nach geordnet (die kleinsten zuerst). Bei Bedarf können durch Anklicken des Buttons "Eigenvektoren" noch die in der Reihenfolge zu den Eigenwerten passenden Eigenvektoren angefordert werden:
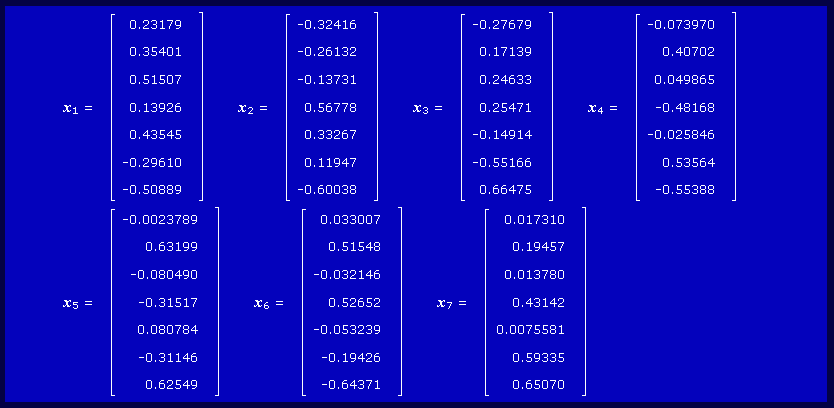

 Für verschiedene Demonstrationen von Aussagen zu Matrizeneigenwertproblemen wird das nachfolgend formulierte Allgemeine Matrizeneigenwertproblem verwendet. Es ist das Finite-Elemente-Modell (mit einer recht groben Diskretisierung mit nur 4 Elementen) des nebenstehend skizzierten Biegeschwingers. Der Träger hat konstanten Querschnitt, so dass auch die Biegesteifigkeit
Für verschiedene Demonstrationen von Aussagen zu Matrizeneigenwertproblemen wird das nachfolgend formulierte Allgemeine Matrizeneigenwertproblem verwendet. Es ist das Finite-Elemente-Modell (mit einer recht groben Diskretisierung mit nur 4 Elementen) des nebenstehend skizzierten Biegeschwingers. Der Träger hat konstanten Querschnitt, so dass auch die Biegesteifigkeit