|
Der Hintergrund des Demonstrationsproblems
 Für verschiedene Demonstrationen von Aussagen zu Matrizeneigenwertproblemen wird das nachfolgend formulierte Allgemeine Matrizeneigenwertproblem verwendet. Es ist das Finite-Elemente-Modell (mit einer recht groben Diskretisierung mit nur 4 Elementen) des nebenstehend skizzierten Biegeschwingers. Der Träger hat konstanten Querschnitt, so dass auch die Biegesteifigkeit EI und die kontinuierliche Massebelegung ρA konstant sind. Für verschiedene Demonstrationen von Aussagen zu Matrizeneigenwertproblemen wird das nachfolgend formulierte Allgemeine Matrizeneigenwertproblem verwendet. Es ist das Finite-Elemente-Modell (mit einer recht groben Diskretisierung mit nur 4 Elementen) des nebenstehend skizzierten Biegeschwingers. Der Träger hat konstanten Querschnitt, so dass auch die Biegesteifigkeit EI und die kontinuierliche Massebelegung ρA konstant sind.
Wie das Matrizeneigenwertproblem für diese Aufgabe erzeugt wird, wird ausführlich auf der Seite "Eigenschwingungen mit der Finite-Elemente-Methode" beschrieben. Nach der Lösung des Allgemeinen Matrizeneigenwertproblems

können die Eigenkreisfrequenzen des Biegeschwingers aus den Eigenwerten λi nach der Formel
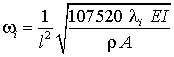
berechnet werden. Die Eigenvektoren, die die Lösung des Matrizeneigenwertproblems liefert, beschreiben die zugehörige Schwingungsform. Das aber ist für die hier zu demonstierenden Aussagen zu den Matrizeneigenwertproblemen uninteressant, trotzdem noch eine Bemerkung zum Berechnungsmodell:
Ein kontinuierlich mit Masse belegter Biegeträger hat unendlich viele Eigenfrequenzen. Die analytische Lösung, die für dieses einfache Problem noch möglich ist, liefert sie alle (wird ausführlich behandelt im Skript "Biegeschwingungen gerader Träger"). Dass das Matrizeneigenwertproblem nur 7 Eigenwerte (und damit 7 Eigenkreisfrequenzen) liefert, liegt an dem recht groben Finite-Elemente-Modell, das allerdings für die Berechnung der kleinsten Frequenzen völlig ausreichend ist.
|















